Network security in the era of Zero Trust architectures requires reliable real-time anomaly detection. In our recent paper presented at IEEE DSAA 2024, we introduce HDSGA (HyperDimensional Streaming Graph Anomaly detection), a novel approach that leverages Hyperdimensional Computing to detect anomalies in computer network traffic with exceptional speed and accuracy.
The Problem
Computer networks naturally represent as dynamic graphs where nodes are endpoints (servers, workstations, devices) and edges are communications between them. Network anomalies - whether from cyberattacks, malware, or intrusions - manifest as unusual patterns in this graph structure: edges that deviate from the baseline topology.
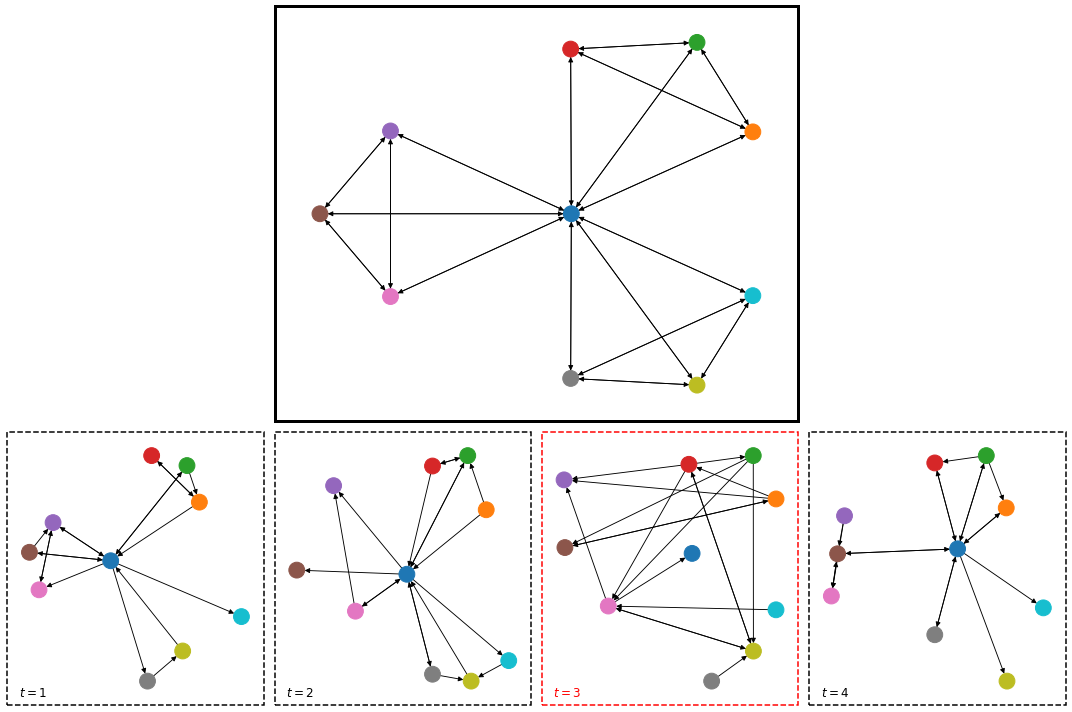
Example of anomaly detection in graph snapshots. The sequence shows snapshots sampled from an underlying windmill graph (t=1, 2, 4). At t=3, the snapshot is sampled from a complete graph and is therefore anomalous.
Traditional anomaly detection faces significant challenges:
- Scale: Real-world networks are extremely large with millions of connections
- Speed: Decisions must be made in real time
- Memory: Storing full network histories is impractical
- Interpretability: Security teams need confidence scores, not just binary predictions
Deep learning models, while powerful, often struggle with the streaming nature of network data and the need for sub-linear memory usage.
Our Approach: Hyperdimensional Computing for Graphs
What is Hyperdimensional Computing?
Hyperdimensional Computing (HDC), also known as Vector Symbolic Architectures, represents information as very high-dimensional vectors (typically 1,000-10,000 dimensions). HDC has shown promise in online learning due to its “embarrassingly parallel” operations and ability to work with symbolic representations.
Graph Encoding with Hypervectors
Our method encodes graph snapshots into hyperdimensional space using the following approach:
- Node Representation: Each network endpoint gets two random binary hypervectors:
- Ĥᵤ represents node u as a source
- Ȟᵤ represents node u as a destination
-
Edge Encoding: A connection from u to v is encoded as the Hadamard product (element-wise multiplication): H̄ᵤᵥ = Ĥᵤ ⊙ Ȟᵥ
-
Graph Snapshot: The complete network state at time t is the weighted sum of all edge encodings:
xₜ = Σ w(u,v)ₜ · Ĥᵤ ⊙ Ȟᵥ
where w(u,v) is the number of communications between u and v
Standardization and Theory
We prove that under reasonable assumptions about the baseline edge-generating process, the standardized encoding follows a known distribution. This allows us to perform non-parametric hypothesis testing to detect anomalies.
The standardized encoding is:
zₜ = (xₜ - E[xₜ]) / √var[xₜ]
When the network behaves normally (edges sampled uniformly), each element of zₜ approximately follows a standard normal distribution.
Anomaly Detection
We compute an anomaly score primitive by counting how many elements of zₜ deviate significantly from expectation:
| s̄ₜ = max(Σ 𝟙{ | zₜ,ᵢ | < θₗ}, Σ 𝟙{ | zₜ,ᵢ | > θᵤ}) |
This captures two types of anomalies:
- Graphs that are more random than baseline (equivalence testing)
- Graphs that are less random than baseline (hypothesis testing)
Confidence Scores
The primitive scores are converted to interpretable Bayesian confidence estimates using a Beta prior. This provides security analysts with probabilistic assessments of whether a network snapshot is anomalous.
The confidence score πₜ tells us: “With probability πₜ, this network activity is anomalous.”
Key Advantages
1. Constant Memory
Unlike methods that store historical data, HDSGA maintains only:
- A (d+1)-dimensional counter vector for score frequencies
- Fixed-size hypervector representations for nodes
This enables deployment on resource-constrained edge devices.
2. Real-Time Operation
The algorithm runs in O(dk) time for k edges and d dimensions. Computation can be further optimized by updating only changed edges.
3. Online Learning
Each snapshot is scored independently - no batch processing required. The confidence estimate updates incrementally as new data arrives.
4. Interpretability
Unlike black-box models, HDSGA provides:
- Probabilistic confidence scores
- Clear anomaly primitives
- Transparent decision logic for security audits
Experimental Results
We evaluated HDSGA on four datasets:
- SIMARGL 2021: 23M observations, 3,886 snapshots
- DARPA 1998: 4.5M observations, 970 snapshots
- APPRAISE H2020: 15M observations, 294 snapshots
- Simulated (TabMT): 80K observations, 303 snapshots
Detection Performance
| Method | Average AUC-ROC | Average AUC-PR |
|---|---|---|
| HDSGA-p | 95.73% | 90.20% |
| HDSGA-c | 93.65% | 85.08% |
| SpotLight | 85.55% | 62.40% |
| AnoGraph | 91.95% | 85.17% |
| MIDAS | 90.84% | 81.69% |
| MIDAS-R | 94.14% | 89.14% |
HDSGA achieved the highest average AUC-ROC across all datasets.
Runtime Performance
On average, HDSGA ran 1.88× faster than the next fastest method. For example, on the SIMARGL dataset:
| Method | Runtime (seconds) |
|---|---|
| HDSGA | 374.9 |
| SpotLight | 543.0 |
| AnoGraph | 1,456.5 |
| MIDAS | 1,352.4 |
| MIDAS-R | 2,392.3 |
Visualization Results
Our experiments on the SIMARGL dataset revealed that different attack types (DoS, port scanning, malware) map to distinct clusters in the hyperdimensional encoding space. This demonstrates that HDSGA not only detects anomalies but also preserves structural information about different types of attacks.
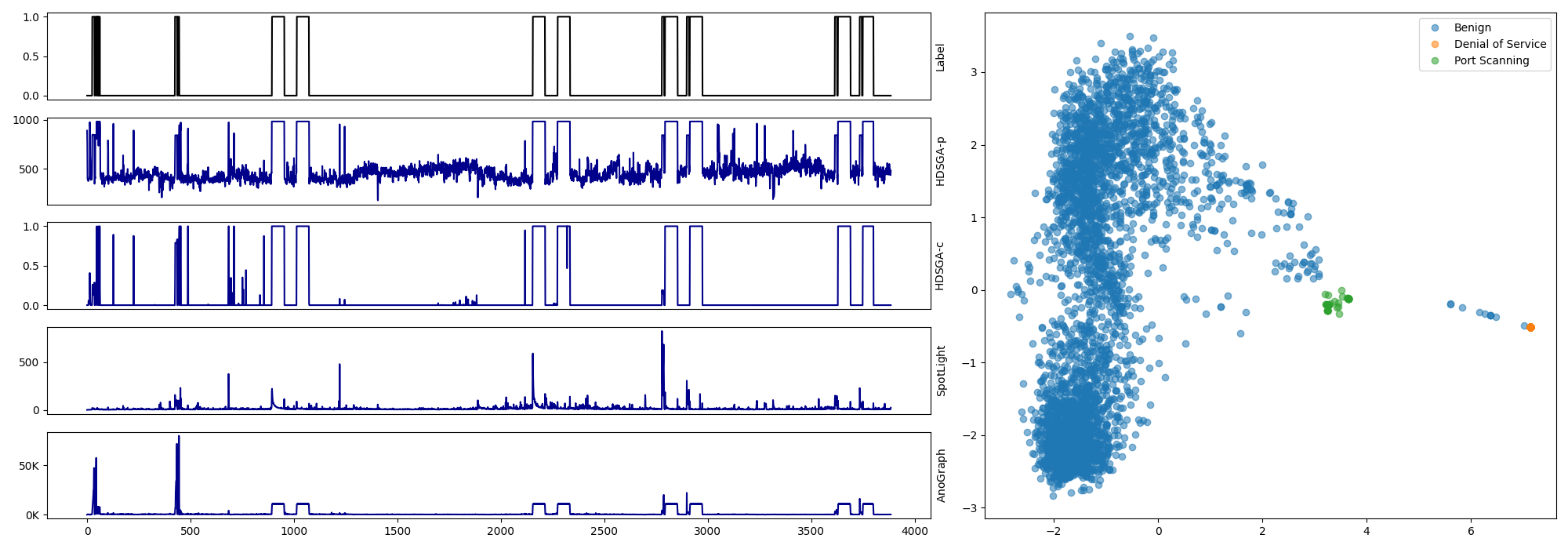
Left: Anomaly detection results on SIMARGL dataset showing ground truth (top row) and detection scores from various methods. Right: 2D projection (PCA) of binary encodings showing how different attack types (DoS, port scanning) cluster separately from benign traffic.
Synthetic Data Insights
We tested HDSGA on synthetic graphs with known structures (complete, caveman, star, wheel, windmill). The encodings successfully distinguished between different graph topologies, with similar structures mapping to nearby regions in the encoding space.
This validates that the hyperdimensional encoding captures meaningful graph properties beyond simple randomness.
Zero Trust Architecture
HDSGA was developed as part of Leidos’ Zero Trust Mission Cloud Initiative. In Zero Trust frameworks, network access is never implicitly trusted - every connection must be verified. Real-time anomaly detection is critical for:
- Behavioral monitoring: Detecting unusual patterns in authorized connections
- Threat hunting: Identifying lateral movement and command-and-control traffic
- Incident response: Rapidly flagging suspicious activity for investigation
HDSGA’s constant memory footprint and real-time operation make it ideal for distributed Zero Trust deployments across large enterprise networks.
Technical Deep Dive: The Mathematics
For those interested in the theoretical foundations, our paper proves several key results:
-
Encoding Distribution: Under uniform sampling, the encoding follows a weighted sum of Bernoulli random variables
-
Central Limit Theorem: The standardized encoding converges to standard normal as dimensionality increases (via Lyapunov CLT)
-
Finite Graph Corrections: We provide exact variance formulas accounting for sampling without replacement in finite networks
These theoretical guarantees ensure that our anomaly detection has well-calibrated false positive rates.
Hyperparameters
The main tuning parameters are:
- p, q: Source and destination mapping probabilities (typically 0.1-0.3)
- θₗ, θᵤ: Lower and upper anomaly thresholds (typically 0-4 standard deviations)
- d: Hypervector dimension (2¹⁰ = 1024 in our experiments)
- γ: Expected contamination rate (fraction of anomalous snapshots)
We provide guidance in the paper for setting these based on empirical percentiles of a small calibration set.
Limitations and Future Work
Current Limitations:
- Assumes baseline generating process exists (though it need not be uniform)
- Very similar graph structures may be confused (e.g., caveman vs. complete graphs)
- Requires bounded edge weights for theoretical guarantees
Future Directions:
- Multi-language support for node identifiers
- Integration with existing SIEM platforms
- Explainability features identifying which edges contribute most to anomaly scores
- Adaptive threshold learning
Implementation
We implemented HDSGA in Python with experiments conducted on AWS WorkSpaces (Amazon Linux 2, 7.7GB RAM, 2.5GHz Intel Xeon). The code leverages:
- NumPy for efficient vector operations
- Sparse representations for memory efficiency
- Parallel processing for large-scale networks
The approach is architecture-agnostic and can be deployed on various platforms from edge devices to cloud infrastructure.
Conclusion
By combining the theoretical foundations of Stochastic Block Models with the computational efficiency of Hyperdimensional Computing, HDSGA provides a practical solution for real-time network anomaly detection. Our results demonstrate that principled mathematical approaches can match or exceed the performance of complex deep learning models while offering superior speed, interpretability, and memory efficiency.
As organizations adopt Zero Trust architectures, tools like HDSGA will become increasingly critical for maintaining security without sacrificing performance.
This research was conducted under Leidos’ Office of Technology Zero Trust Mission Cloud Initiative (approval 24-LEIDOS-0430-27761) and presented at IEEE DSAA 2024.
Read the full paper: IEEE Xplore
